Последнее обновление 21/03/2021
Для простых вещей написать отличный код на Python, используя IDLE или Python Shell, очень даже можно, однако, в больших программных проектах эти инструменты быстро приведут к разочарованию. Интегрированная среда разработкиએ или даже просто хороший редактор кода сделает программирование увлекательным, но только тогда, когда эти инструменты лучшие именно для вас. А какой он для вас лучший?
Я не смогу предложить вам именно то, что соответствует вашему стилю и лучше всего подходит, но объясню плюсы и минусы каждого из них, помогу принять обоснованное решение при выборе. Что-бы было проще, весь список IDE и редакторов кода, которые составляют основу эко‑среды, разделим на две большие категории инструментов: 1) исключительно для разработки на Python, и 2) универсальные, созданные для общей разработки, но которые, однако, могут быть достаточны эффективны для Python.
Прежде чем приступить выполнению КР
Необходимо усвоить и выполнить на практике все упражнения из следующих уроков:
- Интегрированные среды разработки и редакторы кода для Python
- Эффективная среда Python — будь как дома
- Виртуальная среда Python: урок для начинающих
- Pipenv: Руководство по новому инструменту упаковки Python
- Что такое PIP? Руководство начинающего Python-иста
- Менеджер зависимостей Poetry — полный обзор от установки до настройки
Задание №0.
Создаём виртуальную среду для своего проекта
Хотя я не могу гарантировать вам это именно то, что соответствует вашему стилю и лучше всего подходит, но надо с чего-то начинать.
В качестве консоли для работы с Python рекомендую Far Manager. Пройдите по этой ссылке, скачайте (это бесплатно) и следуя инструкциям на этой странице установите. Если вы работаете не в Windows, а в Linux, то встроенного терминала в качестве консоли вполне хватит. И в Windows можно обойтись встроенным cmd, но уж слишком муторно с клавиатуры бродить по папкам, используя встроенные команды вроде cd c:/users/user/.pythonprojects/myproject_2 или mkdir myproject_3. Все эти многочисленные буковки надо записать с клавиатуры. Far Manager избавит вас от этой рутины.
После установки и загрузки вы увидите следующую картинку:
Думаю, что с интерфейсом вы разберетесь самостоятельно и уже через 5 минут сможете спокойно перемещаться между папками файловой системы ОС Windows. Начнем создавать виртуальную среду для своего проекта. По своей сути, основная цель виртуальной среды Python — создание изолированного окружения проектов Python. Это означает, что каждый проект может иметь свои собственные настройки, независимо от того, какие настройки есть у каждого соседнего проекта.
Делай 1
Для начала выберем место, куда вы разместите свой проект:
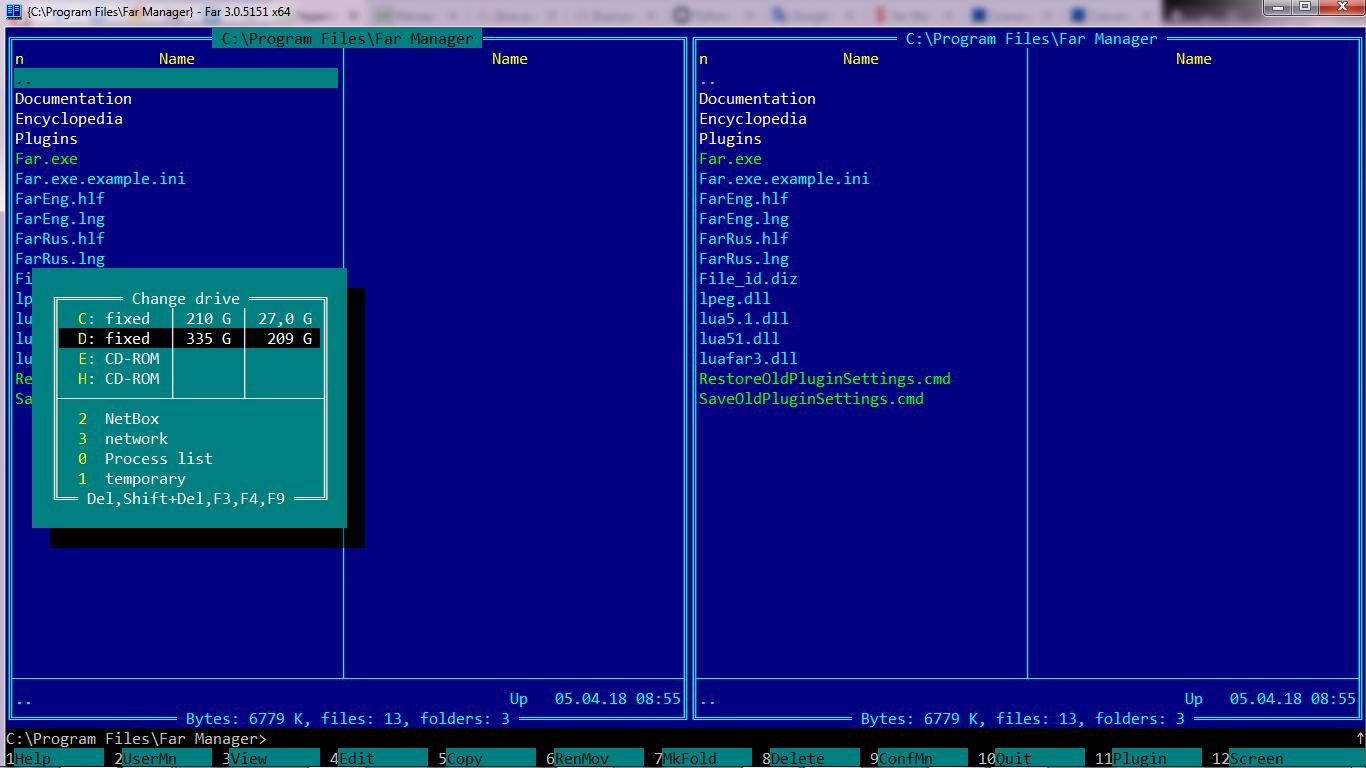
Делай 2
Создаём новую папку для проекта, нажав одновременно клавиши Ctrk+F7, записав имя папки, где будут хранится все файлы проекта и виртуальная среда.
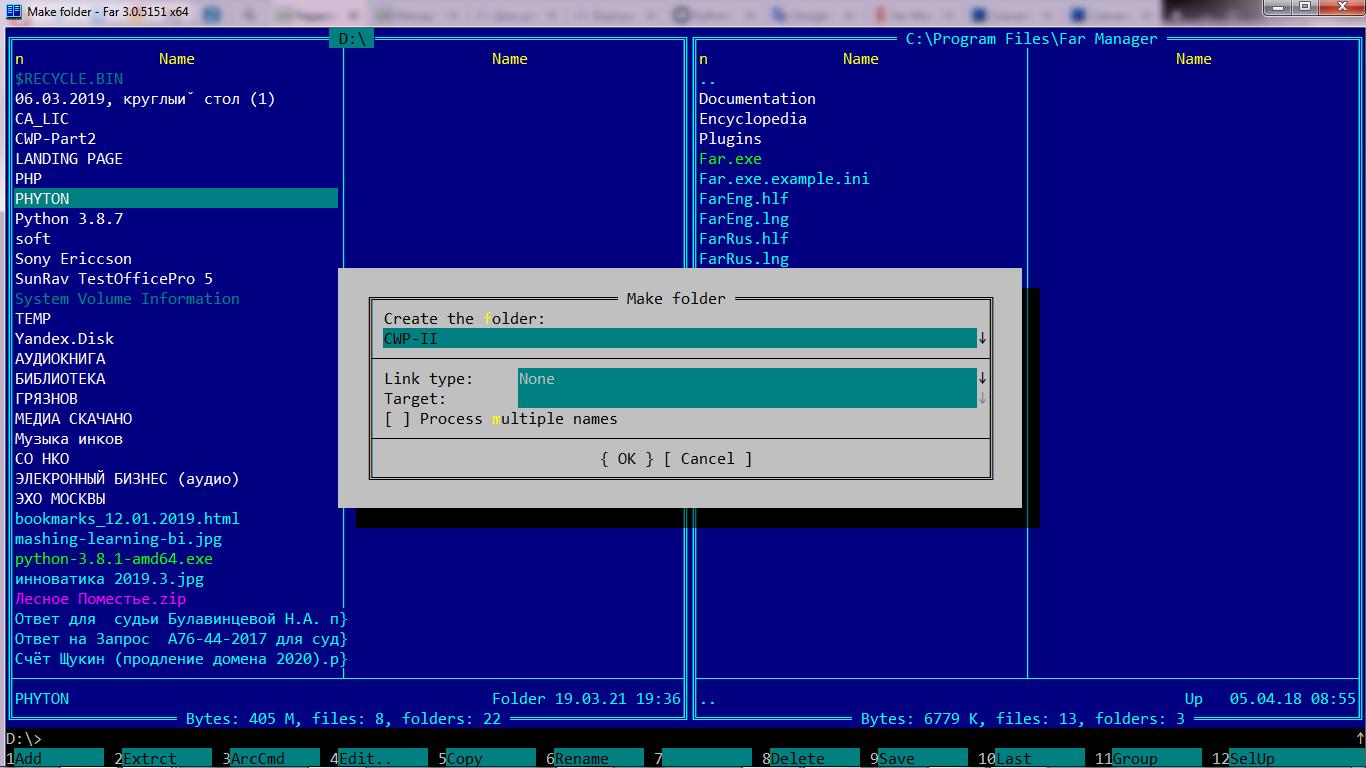
Делай 3
Для того, что-бы наблюдать результата выполнения команд, введённых из командной строки, уберем панели Far Manager. Просто одновременно нажмем клавиши Ctrk+O («О» — это буква, а не цифра).
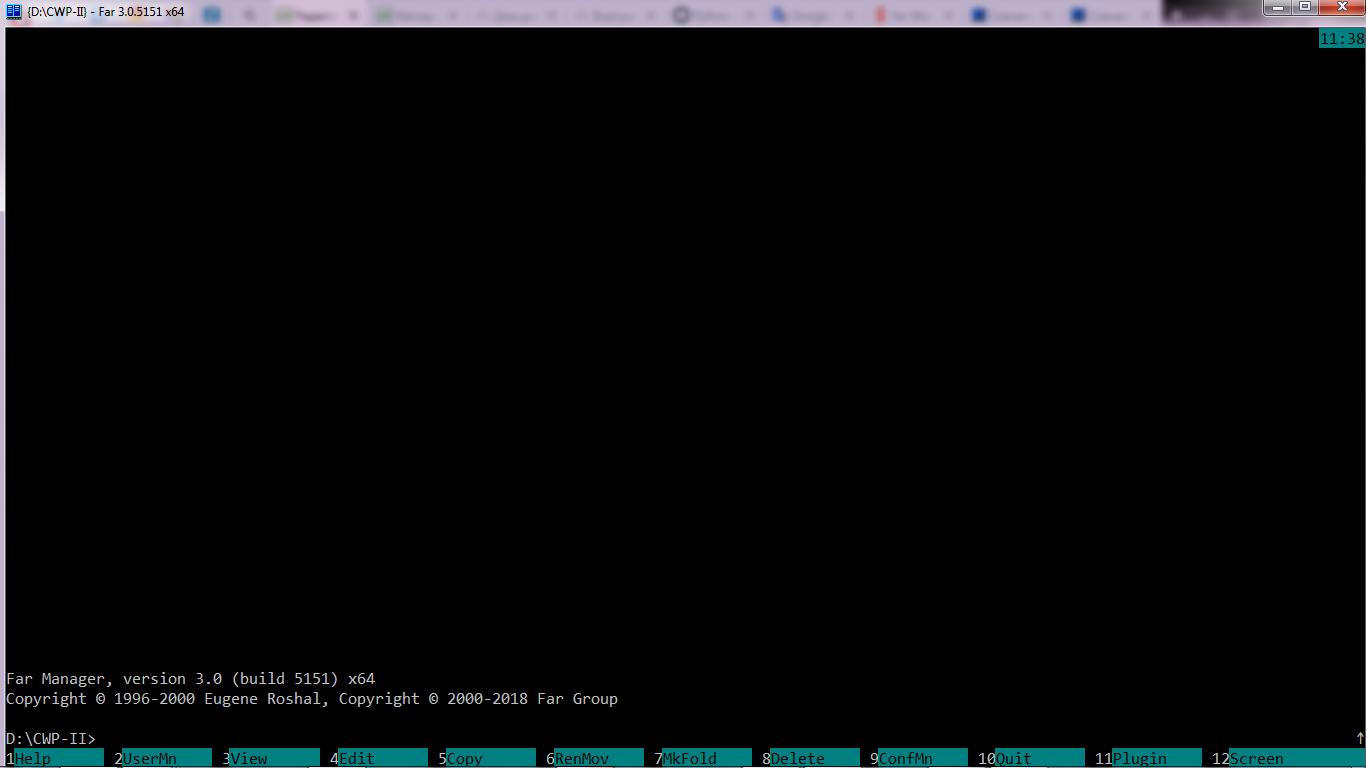
Делай 4
Теперь создадим в папке проекта виртуальную среду Для этого в командной строке консоли запишем:
python3 -m venv env
Для создание виртуальной среды потребуется некоторое время. Когда опять появится строка подсказки консоли, восстановим панели Far Manager, нажав одновременно Ctrk+O.
Делай 5
После создания виртуальной среды в папке вашего проекта появится папка с тем именем, которое вы указали в команде создания, а именно env. Откроем эту папку и увидим следующую архитектуре виртуальной среды. Исследуйте её.
Делай 6
Зайдем в папку scrips виртуальной среды и активируем её загрузив файл activate.bat. Вот теперь ваш проект не будет обращать внимание на соседние проекты и работать только с теми пакетами, которые в нём определены.
Делай 7
Для выполнения курсовой работы вам потребуются два пакета: numpy и matplotlib. Установим их:
pip install numpy matplot
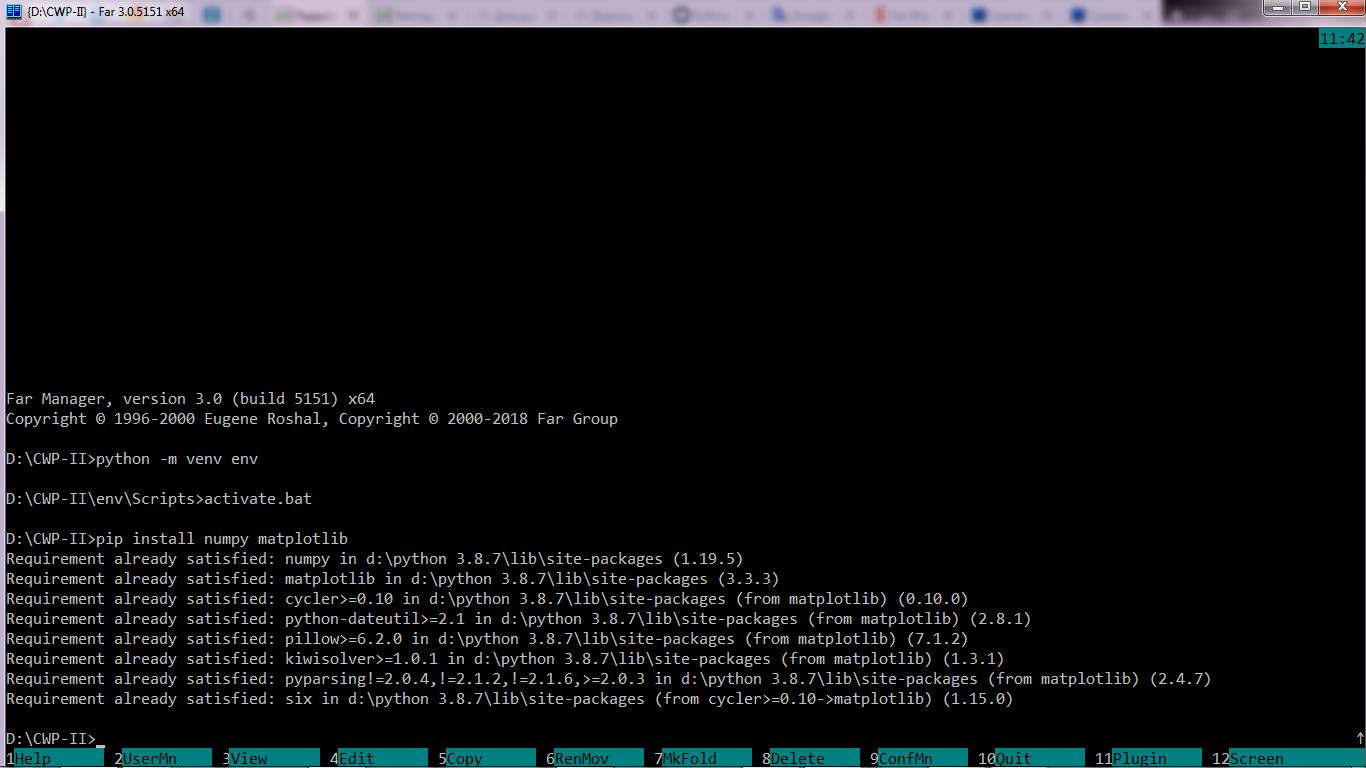
У меня эти пакеты уже установлены для использования в нескольких проектах. Поэтому и сообщение столь лаконично. В вашем случае, когда пакеты не установлены, произойдет их скачивание и официального репозитария PiPy и показаны все этапы установки. то займет некоторое время
Всё теперь готово для плодотворной работы! Можно писать py-файл и сохранять в папке проекта. Когда заканчиваете сеанс работы с текущим проектом, не забывайте деактивировать виртуальную среду. Зайдем в папку scrips виртуальной среды и загрузите файл deactivate.bat.
Отчитываться о своих достижениях не надо — это дело лично ваше и является не только достаточным, но и необходимым условием написания кода для решения задач курсовой работы, т.е. определяет успех выполнения. Если этого не сделать, то дальше продвигаться будет невозможно. Отчитываться не надо, знания проверим тестированием.
Методы сортировки. Часть I
Основой работы является статья Алгоритмы сортировки на Python и приведенные в ней скрипты надо просто повторить.
Задание №1.
Алгоритмы сортировки списков
Цели задания:
- сравнить производительность скриптов, решающих одинаковые задачи на «чистом» Python с производительностью скриптов, использующих метод списков sort(). Для этого необходимо экспериментально получить время выполнения всех скриптов по алгоритмам, описанным в статье. Смею вас уверить цифры у всех будут разные.
- сравнить производительность своих домашних компьютеров и компьютеров в классе 115, используя несколько скриптов, преобразованных в производственную версию (prodaction).
Матричная математика и работа с пакетами. Часть II
Упражнение №1.
Построение графика сигма-функции
"""
Проект: CWP-Part2
Файл: exercise_1.py
Версии: 1.011
Автор и учебная группа: И. Комаров, ЭУ-135
Дата создания: 20.03.2021
Дата последней модификации: 20.03.2021
Зависимости: numpy, matplotlib
Описание: построение графика сигма-функции
Версия Python: 3.8.7
"""
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5, 5, 100)
def sigmoid(alpha):
return 1 / ( 1 + np.exp(- alpha * x))
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi))
plt.plot(x, sigmoid(0.5), color='red')
plt.plot(x, sigmoid(1.0), color='blue')
plt.plot(x, sigmoid(2.0), color='green')
plt.plot(x, sigmoid(3.0), color='yellow')
plt.plot(x, sigmoid(10.0), color='cyan')
plt.legend(['A = 0.5', 'A = 1.0', 'A = 2.0', 'A = 3.0', 'A = 10.0'], loc = 'upper left')
plt.title('Сигмоида')
plt.show()
Упражнение №2.
Получение основных статистических характеристик
"""
Проект: CWP-Part2
Файл: exercise_2.py
Версии: 1.011
Автор и учебная группа: И. Комаров, ЭУ-135
Дата создания: 20.03.2021
Дата последней модификации: 20.03.2021
Зависимости: numpy, matplotlib
Описание: Получение основных статистических характеристик
Версия Python: 3.8.7
"""
import matplotlib.pyplot as plt
import numpy as np
import math
ones = np.ones(100)
rnd = np.random.random(100) * 0.8
samples = ones + rnd
print('Массив для упражнений:\n', samples)
# Посчитаем среднее:
print('\nAverage: ', np.average(samples))
print('Mean: ', np.mean(samples))
# Медиану:
print('\nМедиана: ', np.median(samples))
# Процентили:
print('\nПроцентиль, 50%: ', np.percentile(samples, 50))
print('Процентиль, 95%: ', np.percentile(samples, 95))
print('Процентиль, 99%: ', np.percentile(samples, 99))
# Максимум, минимум, peak-to-peak:
print('\nМаксимум: ', samples.max())
print('Минимум: ', samples.min())
print('Диапазон: ', samples.ptp())
# А заодно уж и стандартное отклонение с дисперсией:
print('\nСтандартное отклонение: ', np.std(samples))
print('Дисперсия: ', np.var(samples))
print('Дисперсия (проверим): ', pow(np.std(samples), 2))
# Использованная выше функция np.random.random генерирует случайные числа с
# равномерным распределением. А если мы хотели бы использовать нормальное
# распределение? Нет проблем:
samples = np.random.normal(loc=0, scale=5, size=100000)
plt.hist(samples, 200)
plt.show()
Упражнение №3.
Матричные операции
"""
Проект: CWP-Part2
Файл: exercise_3.py
Версии: 1.011
Автор и учебная группа: И. Комаров, ЭУ-135
Дата создания: 20.03.2021
Дата последней модификации: 20.03.2021
Зависимости: numpy, matplotlib
Описание: Матричные операции
Версия Python: 3.8.7
"""
import numpy as np
import numpy.matlib
import numpy.linalg
m1 = np.arange(1, 10).reshape(3,3)
print('Первая матрица\n', m1)
m2 = np.identity(3)
print('\nВторая матрица\n', m2)
# Транспонируем первую матрицу, а также посчитаем след и детерминант второй:
print('\nТранспонируем первую матрицу\n', m1.transpose())
print('\nСлед второй матрицы ', m2.trace())
det = np.linalg.det(m2)
print('\nОпределитель второй матрицы ', det)
# Матрицы можно складывать, умножать на число, умножать на вектор, а также
# умножать на другую матрицу:
print('\nСложим две матрицы\n', m1 + m2)
print('\nУмножим первую матрицу на число 3\n', m1 * 3)
m1 + np.array([1,2,3])
print('\nПеремножим матрицы\n', m1 * m2)
# Посчитать матрицу, обратную к данной, можно функцией np.linalg.inv:
m3 = np.matlib.rand(3, 3)
print('\nТретья матрица\n', m3)
# (m3 * np.linalg.inv(m3))
print('\nОбратим третью матрицу и умеожим на себя\n', (m3 * np.linalg.inv(m3)).round())
Задание №2.
Работа с двумерными массивами (матрицами)
Для начала понимания, как работать с матрицами решите следующие задачи, количеством 31. Их можно записать в одном проекте. Эти задачи соответствуют задачам от 67 до 97 в вашем предыдущем задании.
При решении задач использовать NumPy: справочное руководство
Цели задания:
- сравнить производительность скриптов, решающих одинаковые задачи на «чистом» Python с производительностью скриптов, использующих пакет Numpy. Для этого необходимо экспериментально получить время выполнения всех скриптов по алгоритмам предыдущего задания и новых скриптов. Смею вас уверить цифры у всех будут разные.
- сравнить производительность своих домашних компьютеров и компьютеров в классе 115, используя несколько скриптов, преобразованных в производственную версию (production).
Задачи:
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Найти наибольший элемент столбца матрицы A, для которого сумма абсолютных значений элементов максимальна.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Найти наибольшее значение среди средних значений для каждой строки матрицы.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Найти наименьший элемент столбца матрицы A, для которого сумма абсолютных значений элементов максимальна.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Найти наименьшее значение среди средних значений для каждой строки матрицы.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Определить средние значения по всем строкам и столбцам матрицы. Результат оформить в виде матрицы из N + 1 строк и M + 1 столбцов.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Найти сумму элементов всей матрицы. Определить, какую долю в этой сумме составляет сумма элементов каждого столбца. Результат оформить в виде матрицы из N + 1 строк и M столбцов.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Найти сумму элементов всей матрицы. Определить, какую долю в этой сумме составляет сумма элементов каждой строки. Результат оформить в виде матрицы из N строк и M+1 столбцов.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Определить, сколько отрицательных элементов содержится в каждом столбце и в каждой строке матрицы. Результат оформить в виде матрицы из N + 1 строк и M + 1 столбцов.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Определить, сколько нулевых элементов содержится в верхних L строках матрицы и в левых К столбцах матрицы.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Перемножить элементы каждого столбца матрицы с соответствующими элементами K-го столбца.Аим
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Просуммировать элементы каждой строки матрицы с соответствующими элементами L-й строки.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Разделить элементы каждой строки на элемент этой строки с наибольшим значением.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Разделить элементы каждого столбца матрицы на элемент этого столбца с наибольшим значением.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Разделить элементы матрицы на элемент матрицы с наибольшим значением.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Все элементы имеют целый тип. Дано целое число H. Определить, какие столбцы имеют хотя бы одно такое число, а какие не имеют.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Исключить из матрицы строку с номером L. Сомкнуть строки матрицы.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Добавить к матрице строку и вставить ее под номером L.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Найти сумму элементов, стоящих на главной диагонали, и сумму элементов, стоящих на побочной диагонали (элементы главной диагонали имеют индексы от [0,0] до [N,N], а элементы побочной диагонали – от [N,0] до [0,N]).
- Создать квадратную матрицу A, имеющую N строк и N столбцов со случайными элементами. Определить сумму элементов, расположенных параллельно главной диагонали (ближайшие к главной). Элементы главной диагонали имеют индексы от [0,0] до [N,N].
- Создать квадратную матрицу A, имеющую N строк и N столбцов со случайными элементами. Определить произведение элементов, расположенных параллельно побочной диагонали (ближайшие к побочной). Элементы побочной диагонали имеют индексы от [N,0] до [0,N].
- Создать квадратную матрицу A, имеющую N строк и N столбцов со случайными элементами. Каждой паре элементов, симметричных относительно главной диагонали (ближайшие к главной), присвоить значения, равные полусумме этих симметричных значений (элементы главной диагонали имеют индексы от [0,0] до [N,N]).
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Исходная матрица состоит из нулей и единиц. Добавить к матрице еще один столбец, каждый элемент которого делает количество единиц в каждой строке чётным.
- Создать квадратную матрицу A, имеющую N строк и N столбцов со случайными элементами. Найти сумму элементов, расположенных выше главной диагонали, и произведение элементов, расположенных выше побочной диагонали (элементы главной диагонали имеют индексы от [0,0] до [N,N], а элементы побочной диагонали — от [N,0] до [0,N]).
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Дан номер строки L и номер столбца K, при помощи которых исходная матрица разбивается на четыре части. Найти сумму элементов каждой части.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Определить, сколько нулевых элементов содержится в каждом столбце и в каждой строке матрицы. Результат оформить в виде матрицы из N + 1 строк и M + 1 столбцов.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Дан номер строки L и номер столбца K, при помощи которых исходная матрица разбивается на четыре части. Найти среднее арифметическое элементов каждой части.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Все элементы имеют целый тип. Дано целое число H. Определить, какие строки имеют хотя бы одно такое число, а какие не имеют.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Исключить из матрицы столбец с номером K. Сомкнуть столбцы матрицы.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Добавить к матрице столбец чисел и вставить его под номером K.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Добавить к элементам каждого столбца такой новый элемент, чтобы сумма положительных элементов стала бы равна модулю суммы отрицательных элементов. Результат оформить в виде матрицы из N + 1 строк и M столбцов.
- Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами. Добавить к элементам каждой строки такой новый элемент, чтобы сумма положительных элементов стала бы равна модулю суммы отрицательных элементов. Результат оформить в виде матрицы из N строк и M + 1 столбцов.
Бонус
Практически все задачи начинаются со слов Создать прямоугольную матрицу A, имеющую N строк и M столбцов со случайными элементами или чего-то подобного. Вот вам код, который полностью решает эту задачу:
"""
Проект: CWP-Part2
Файл: random_matrix.py
Версии: 1.011
Автор и учебная группа: В.В. Костерин
Дата создания: 21.03.2021
Дата последней модификации: 21.03.2021
Зависимости: numpy
Описание: Генератор матрицы со случайными значениями
Версия Python: 3.8.7
"""
import numpy as np
N = 10
M = 12
print(f'\nЗадан размер матрицы случайных целых чисел: [{N}, {M}]')
""" Инициализируем генератор """
np.random.seed(0)
matrix = np.random.randint(100, size = (N, M))
print('\nПрямоугольная матрица случайных целых чисел:\n', matrix)
matrix = np.random.random(size = (N, M))
print('\nПрямоугольная матрица случайных действительных чисел в диапазоне [0, 1]\n с нормальным законом распределения:\n', matrix)
matrix = np.random.random(size = (N, M)) * 10
print('\nПрямоугольная матрица случайных действительных чисел в диапазоне [0, 10]\n с нормальным законом распределения:\n', matrix)
matrix = np.random.random(size = (N, M)) * 100
print('\nПрямоугольная матрица случайных действительных чисел в диапазоне [0, 100]\n с нормальным законом распределения:\n', matrix)
"""
Аналогично с использованим кземпляра класса RandomState.
Сравните полученные значения и поиграйте с аргументом инициализации генератора
"""
rng = np.random.RandomState(0)
print('\nСОЗДАН ЭКЗЕМПЛЯР КЛАССА RandomState()\n')
matrix = rng.randint(100, size = (N, M))
print('\nПрямоугольная матрица случайных целых чисел:\n', matrix)
matrix = rng.random(size = (N, M))
print('\nПрямоугольная матрица случайных действительных чисел в диапазоне [0, 1]\n с нормальным законом распределения:\n', matrix)
matrix = rng.random(size = (N, M)) * 10
print('\nПрямоугольная матрица случайных действительных чисел в диапазоне [0, 10]\n с нормальным законом распределения:\n', matrix)
matrix = rng.random(size = (N, M)) * 100
print('\nПрямоугольная матрица случайных действительных чисел в диапазоне [0, 100]\n с нормальным законом распределения:\n', matrix)
Упражнение №4.
Решение СЛАУ методом Гаусса
"""
Проект: CWP-Part2
Файл: exercise_4.py
Версии: 1.011
Автор и учебная группа: И. Комаров, ЭУ-135
Дата создания: 20.03.2021
Дата последней модификации: 20.03.2021
Зависимости: numpy, matplotlib
Описание: решение СЛАУ методом Гаусса
Версия Python: 3.8.7
"""
myA = [
[1.0, -2.0, 3.0, -4.0],
[3.0, 3.0, -5.0, -1.0],
[3.0, 0.0, 3.0, -10.0],
[-2.0, 1.0, 2.0, -3.0]
]
myB = [
2.0,
-3.0,
8.0,
5.0]
""" вывод системы на экран """
def FancyPrint(A, B, selected):
for row in range(len(B)):
print("(", end='')
for col in range(len(A[row])):
print("\t{1:10.2f}{0}".format(" " if (selected is None or selected != (row, col)) else "*", A[row][col]), end='')
print("\t) * (\tX{0}) = (\t{1:10.2f})".format(row + 1, B[row]))
""" перемена местами двух строк системы """
def SwapRows(A, B, row1, row2):
A[row1], A[row2] = A[row2], A[row1]
B[row1], B[row2] = B[row2], B[row1]
""" деление строки системы на число """
def DivideRow(A, B, row, divider):
A[row] = [a / divider for a in A[row]]
B[row] /= divider
""" сложение строки системы с другой строкой, умноженной на число """
def CombineRows(A, B, row, source_row, weight):
A[row] = [(a + k * weight) for a, k in zip(A[row], A[source_row])]
B[row] += B[source_row] * weight
""" решение системы методом Гаусса (приведением к треугольному виду) """
def Gauss(A, B):
column = 0
while (column < len(B)):
print("Ищем максимальный по модулю элемент в {0}-м столбце:".format(column + 1))
current_row = None
for r in range(column, len(A)):
if current_row is None or abs(A[r][column]) > abs(A[current_row][column]):
current_row = r
if current_row is None:
print("решений нет")
return None
"""FancyPrint(A, B, (current_row, column)) """
if current_row != column:
print("Переставляем строку с найденным элементом повыше:")
SwapRows(A, B, current_row, column)
"""FancyPrint(A, B, (column, column)) """
print("Нормализуем строку с найденным элементом:")
DivideRow(A, B, column, A[column][column])
"""FancyPrint(A, B, (column, column)) """
print("Обрабатываем нижележащие строки:")
for r in range(column + 1, len(A)):
CombineRows(A, B, r, column, -A[r][column])
"""FancyPrint(A, B, (column, column)) """
column += 1
print("Матрица приведена к треугольному виду, считаем решение")
X = [0 for b in B]
for i in range(len(B) - 1, -1, -1):
X[i] = B[i] - sum(x * a for x, a in zip(X[(i + 1):], A[i][(i + 1):]))
print("Получили ответ:")
print("\n".join("X{0} =\t{1:10.2f}".format(i + 1, x) for i, x in enumerate(X)))
return X
print("Исходная система:")
FancyPrint(myA, myB, None)
import time
begtime = time.perf_counter()
Gauss(myA, myB)
endtime = time.perf_counter()
print('\nВремя выполнения, с:', endtime-begtime)
Упражнение №5.
Решение СЛАУ методом Гаусса с использованием Numpy
"""
Проект: CWP-Part2
Файл: exercise_5.py
Версии: 1.011
Автор и учебная группа: И. Комаров, ЭУ-135
Дата создания: 20.03.2021
Дата последней модификации: 20.03.2021
Зависимости: numpy, matplotlib
Описание: решение СЛАУ методом Гаусса
Версия Python: 3.8.7
"""
import numpy # импортируем библиотеку
""" исходные данные """
myA = [
[1.0, -2.0, 3.0, -4.0],
[3.0, 3.0, -5.0, -1.0],
[3.0, 0.0, 3.0, -10.0],
[-2.0, 1.0, 2.0, -3.0]
]
myB = [
2.0,
-3.0,
8.0,
5.0]
"""
вывод системы на экран
def FancyPrint(A, B, selected):
for row in range(len(B)):
print("(", end='')
for col in range(len(A[row])):
print("\t{1:10.2f}{0}".format(" " if (selected is None or selected != (row, col)) else "*", A[row][col]),
end='')
print("\t) * (\tX{0}) = (\t{1:10.2f})".format(row + 1,
B[row]))
"""
print("Система линейных уравнений:")
print("Матрица левых частей:\n", myA)
print("Вектор правой части:", myB)
#print("Система линейных уравнений:")
#FancyPrint(myA, myB, None)
import time
begtime = time.perf_counter()
slv = numpy.linalg.solve(myA, myB)
endtime = time.perf_counter()
print("\nРешение:")
print(slv)
print('\nВремя выполнения, с:', endtime-begtime)

Ваш комментарий будет первым